§ 6. Парадокс лысого

Заканчивая этот раздел, посвященный индукции и ее видам, хотелось бы отметить, что проблема индукции как особой мыслительной операции до сих пор таит в себе множество неясностей и неоднозначностей. Некоторые философы, как например английский философ Карл Поппер, вообще отрицали индукцию как прием и метод научного познания. По-видимому, дело здесь в большом значении дополнительных методов обоснования, необходимых для полноценного использования индукции. Как мы видели, сама по себе индукция в чистом виде – в форме популярной индукции - вряд ли носит научный характер и всегда так или иначе должна подкрепляться еще чем-то. Необходимость в такого рода дополнительных подкреплениях индуктивного вывода и малая ясность общей логики их использования, по-видимому, и порождает повышенную проблемность индукции как логического вывода сравнительно с выводом дедуктивным.

Для иллюстрации проблемности даже, казалось бы, такого наиболее обоснованного ее вида, как математическая индукция, проинтерпретируем в ее терминах так называемый «парадокс лысого», известный еще со времен античной науки и философии.

Допустим, есть некий лысый человек, который применяет настолько замечательное лекарство против облысения, что оно каждый день прибавляет к его лысине по одному волосу. Перестанет ли в этом случае человек быть когда-нибудь лысым ? Кажется, что да. Если прибавлять каждый день по одному волосу, то рано или поздно лысина исчезнет и человек перестанет быть лысым. Но попробуем сформулировать это утверждение в виде математической индукции.

Пусть свойство Р – свойство «быть видимо лысым». Тогда Р(ч) есть утверждение «человек (ч) видимо лысый», т.е. лысый, если смотреть на его голову обычными глазами с некоторого расстояния. Пусть далее n – человек с числом волос на голове, равных числу n, которое добавилось к первоначальной лысине человека спустя n дней. Здесь мы можем доказать следующее:

1. Базис индукции: Р(1) – человек с одним волосом на голове видимо лыс. Это кажется очевидным.

2. Индуктивное предположение: пусть будет верно, что P(n), т.е., что человек с n числом волос на голове видимо лыс. Тогда ясно, что добавление одного волоса не сделает в этом случае человека видимо не лысым, т.е. верным будет и P(n+1). Следовательно, если P(n), то P(n+1) – мы доказываем индуктивное предположение.

Теперь, если мы принимаем аксиому математической индукции, мы обязаны сделать вывод: для любого n верно P(n), т.е. человек будет видимо лысым при любом числе волос у него на голове, что явно представляет из себя нелепицу!

Проблема здесь состоит в том, что состояние «быть видимо лысым» определяется особым состоянием количества – зрительно воспринимаемым числом волос, которое проявляет неоднозначные свойства, не вполне вписывающиеся в поведение обычных чисел.

В современной математике есть теория так называемых нечетких понятий. Например, такое понятие, как «вечер» - это пример нечеткого понятия. В самом деле, что такое вечер? Это 17 часов? 20 часов? Или 21 час? Или это время с 18 до 21 часа? А может быть, с 19 до 23 часов? Так точно ответить нельзя. Нельзя точно указать час, или временной интервал, который называется «вечер». Вот почему это нечеткое понятие, в отличие, например, от понятия «17 часов». Однако оказывается, что с нечеткими понятиями все же можно работать достаточно четко, и даже можно построить логику таких понятий. Давайте соберем 1000 человек и каждого попросим ответить на вопрос «Укажите три ближайших часа, которые точно, с вашей точки зрения, относятся к понятию «вечер»», указав в качестве возможных ответов все часы суток. Тогда один человек может указать 17-18-19 часов, другой – 19-20-21 час, и т.д. Теперь соберем все эти ответы и составим график, в котором по горизонтальной оси будут отложены часы суток от 0 до 24 часов, по вертикальной линии – доля людей, которые указали в качестве «вечера» тот или иной час. У нас получится, по-видимому, некоторая кривая, которая будет равна нулю в утренние и дневные часы, а ближе к 17-18 часам начнет подниматься, достигая единицы, и затем вновь падая к ночным часам. Так вот, теперь можно сказать, что нечеткое понятие «вечер» - это такое понятие, которое распределено степенями выраженности по множеству четких понятий (в данном случае по часам суток). Таковы же понятия «утро», «день», «здоровье», «болезнь» и т.д. Мы-то как раз постоянно используем разные нечеткие понятия и хорошо понимаем друг друга. Современная математика также научилась работать с такими понятиями, приблизившись к пониманию работы обычного человеческого сознания. Давайте теперь с точки зрения нечетких понятий вернемся к парадоксу лысого.

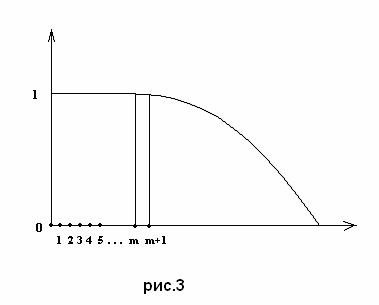
В этом парадоксе мы как раз имеем дело с нечетким понятием «видимо лысый». Что такое «видимо лысый»? Это человек с 15 волосами на голове? С 2 волосами? Или может быть и при 75 волосах на голове можно быть видимо лысым? Ясно, что однозначно на эти вопросы ответить нельзя, так что в этом случае мы вновь имеем дело с нечетким понятием «видимо лысый». Такое понятие также будет характеризоваться некоторой кривой своих степеней выраженности по числу волос. Ясно, что эта кривая будет равняться единице при числе волос, равном 0. Потом она может подержаться на единице до некоторого числа m волос и затем начнет падать, устремляясь к нулю с дальнейшим ростом волос на голове (см. рис.3).

Нечеткое понятие «видимо лысый» можно выразить как свойство Р («быть видимо лысым»). Это свойство есть нечеткое свойство, выражающее нечеткое понятие. Теперь зададим вопрос: как выглядит схема математической индукции по отношению к нечетким свойствам? Выполняется ли вообще такая индукция в этом случае? А если выполняется, то не возникнет ли некоторых ограничений, очерчивающих условия ее выполнимости?

Чтобы ответить на эти вопросы, вернемся вновь к формулировке посылок математической индукции для свойства «быть видимо лысым».

1. Базис индукции: Р(1) – человек с одним волосом на голове видимо лыс. С этим по-прежнему можно согласиться. Кривая степеней выраженности нечеткого свойства Р в данном случае такова, что на одном волосе она еще равна единице.

2. Индуктивное предположение: Пусть будет верно, что P(n), т.е. человек с n волосами на голове еще видимо лыс, т.е. степень выраженности нечеткого свойства Р на числе волос n еще равна единице. Можно ли отсюда вывести P(n+1) ? И вот здесь мы видим проблему. Если, например, n – это то самое число волос m, начиная с которого кривая Р начинает падать, то при еще выполнении свойства P(m) уже не будет полностью выполнено свойство P(m+1), и мы не сможем утверждать P(m+1), поскольку такая запись предполагает полное выполнение свойства Р на m+1 волосах, т.е. равенство кривой Р единице на m+1.

Таким образом, мы видим, что индуктивное предположение для случая нечетких свойств (понятий) в общем виде не выполняется. Правда, не стоит отсюда делать слишком поспешный вывод о полной неприменимости математической индукции для нечетких свойств. Например, до числа m индуктивное предположение было бы выполнено. Интервал (в нашем примере это [0,m]), на котором нечеткое свойство Р принимает значение 1, можно было бы называть индуктивным интервалом. В рамках этого интервала схема математической индукции выполняется. Отсюда же можно лучше понять условия применимости классического случая математической индукции. Она может применяться только для четких свойств с бесконечным индуктивным интервалом. Выполнение базиса и индуктивного предположения математической индукции оказывается в этом случае одновременно определением именно таких условий.

Уже на этом примере читатель мог убедиться, сколь не проста и далека от своего окончательного разрешения проблема индукции. 

Вопросы к 1-й главе

1. Пусть в палате № 7 находятся пять больных. Сформулируйте возможные случаи

    полной перечислительной индукции для этой ситуации.

2. Приведите пример популярной неполной энумеративной индукции из

    медицинской практики и ее более строгого обоснования в медицинской теории.

3. Является ли вывод «Если лекарство помогало в прошлом, то оно поможет и в

    следующий раз» выводом по индукции? Опишите логическую структуру этого

    умозаключения и его возможную обоснованность.

4. Является ли вывод «Если лекарство помогло одному больному, то оно поможет и другому» выводом по аналогии? Опишите его логическую структуру.